밑바닥부터 만들면서 배우는 LLM 책을 이어서 2.5 바이트 페어 인코딩부터 2.7 토큰 임베딩 과정까지 읽으면서 떠오른 질문들을 정리해보았습니다.

1. 바이트 페어 인코딩 (Byte Pair Encoding, BPE) 톺아보기
- 질문
- BPE 작동 원리 및 기준
- BPE 사전을 구성하는 기본 단어 혹은 부분 단어는 어떤 기준으로 선정하는가?
- 개별 문자도 사전에 포함된다는데 그게 의미가 있나?
- 부분 단어로 쪼갠 결과가 훈련에 따라 달라질 수 있다는데 BPE 도 훈련을 거치나?
- 사전(Vacab) 구축 데이터와 한국어 처리 방식
- 사전을 구축할 때 어느 정도 크기의, 어떤 데이터셋을 사용하는가?
- 한글은 사전에 포함되는가?
- 한글은 분해하는 단위가 무엇인가? (음절 vs 자모)
- 토큰 형태와 모델 성능의 상관관계
- 단어가 통으로(Whole word) 들어가는 것이 예측 성능이나 효율성에 이점을 주는지?
- BPE 작동 원리 및 기준
- 답변 요약
- BPE 작동 원리: 빈도 기반 병합
- 가장 자주 등장하는 문자 쌍을 합치는 "통계적 빈도"가 기준이며, 병합 규칙을 만드는 훈련 과정을 거침.
- 개별 문자는 모르는 단어(OOV)가 나왔을 때 처리를 포기하지 않고 쪼개서라도 읽기 위한 안전장치임.
- 데이터셋 및 한글 처리
- 사전학습과 동일한 데이터 셋을 사용하되, 샘플링을 통해 일부만 추출하여 사전 구축에 사용.
- 한글을 포함한 모든 언어가 사전에 포함되나, 빈도가 높은 영어와 코드가 대부분을 차지하고 한글 등은 상대적으로 불리함(잘게 쪼개짐). 사전에 없더라도 바이트 단위 분해를 통해 표현 자체는 가능함.
- 한글은 주로 음절 단위로 처리하되 희귀어는 자모가 아닌 바이트 단위로 쪼갬.
- 성능 영향: 통 단어가 유리함
- 단어가 통으로 토큰화되면 의미 파악(개념 연결), 긴 문맥 기억(Context Window), 처리 속도 및 비용 면에서 훨씬 효율적.
- 반면, 너무 잘게 쪼개지면 연산 낭비가 발생하고 모델의 이해도가 떨어질 수 있음.
- BPE 작동 원리: 빈도 기반 병합
사전에 존재하지 않는 단어가 나타났을 때 <unknown> 토큰으로 치환하는 대신 BPE를 이용해 바이트 단위로 나눠서 처리한다는 아이디어는 이해했지만 세부적인 구현에 대해 설명하지 않아 떠오른 궁금증들을 질문했습니다. 그런데 저와 같은 생각을 한 사람이 많은지 깃허브 실습 코드를 보면 BPE 알고리즘을 직접 만드는 실습도 존재합니다. 이 실습도 진행해보고 글로 정리할 예정입니다.
작동 원리에 대해 질문과 답변을 주고 받다보니 문득 한글, 한자 등의 문자들은 어떻게 처리하는지 궁금했습니다. 알파벳은 문자 단위로 쪼개는 것이 명확한데 한글은 자음, 모음, 받침이 한 글자를 이루기 때문에 어떻게 쪼갤지 쉽게 상상이 되지 않았습니다. 이 역시 바이트 단위로 쪼갠다는 답변을 듣고, 바이트 단위까지 쪼개진 토큰이 나중에 문맥 정보를 담는 벡터가 될텐데 그런 작은 단위의 글자에 문맥을 포함한 "정보"가 존재할까 하는 의문도 생겼습니다. 이런 의문은 책의 뒷부분을 더 읽어보고 다시 고민해볼 예정입니다.
2. LLM 학습 방식에 따른 입력/타깃 텐서 구성 전략
- 질문
- 책에 나온 "입력 텐서를 한 칸씩 밀어서 타깃 텐서를 만드는(Next Token Prediction)" 방식 외에 다른 데이터 준비 방법이 있는지?
- 이 방식이 가장 간단해서 사용하는 것인지, 아니면 다른 목적을 가진 데이터 세팅 방식들도 존재하는지?
- 답변 요약
- 책의 방식은 Causal Language Modeling(CLM)이라 부르며, GPT와 같은 생성형 모델을 만들기 위한 표준 방식임.
- 모델의 목적(이해 vs 생성)에 따라 데이터를 구성하는 다른 대표적인 방식들이 존재함:
- 빈칸 채우기 (MLM): 문장 중간을 가리고 맞히는 방식 (예: BERT). 문맥 이해와 분류에 강점.
- 복원하기 (Seq2Seq): 뒤섞이거나 훼손된 문장을 입력받아 온전한 문장으로 복구하는 방식 (예: T5). 번역 및 요약에 강점.
입력-타깃 쌍들을 담은 텐서를 모아서 파이토치의 DataSet, DataLoader를 구성할 때 책에서는 "가장 쉬운 방법"이라는 표현을 사용했습니다. 가장 쉽다고 하니 다른 방법도 존재하는 것인가 궁금증이 생겨 Gemini에게 물어보았고, 모델의 목적에 따라 데이터 세팅이 달라진다는 어찌보면 당연한 대답을 들었습니다.
3. 훈련 과정에서의 배치 크기와 트레이드오프
- 질문
- 일반적인 개발에서 병렬 처리를 해도 결과값이 같은데, LLM 훈련에서는 왜 배치 크기를 바꾸면 결과가 달라지는지?
- 배치 크기가 단순 속도/처리량 문제가 아니라, 모델 성능에 영향을 주는 하이퍼 파라미터(트레이드오프)인 이유는?
- 답변 요약
- 사전 훈련은 데이터 묶음(Batch)의 평균값(통계)을 이용해 수식 자체를 수정하는 과정이므로 묶는 크기에 따라 학습 방향이 달라짐.
- 배치 크기에 따른 트레이드오프:
- 작은 배치: 방향이 불안정(Zigzag)하지만, 그 불확실성(Noise) 덕분에 일반화 성능이 좋고 가짜 정답(Local Minima)을 탈출하기 유리함.
- 큰 배치: 통계적으로 안정적이고 GPU 연산 효율이 좋아 속도가 빠르지만, 너무 정직하게 학습되어 최적의 해를 놓칠 위험이 있음.
서버 개발자로서 "배치" 작업이라는 말을 들으면 실시간 스트림 처리에 대비되는 단어로서 대량의 데이터를 한 번에 모아서 처리하는 자동화 작업을 떠올립니다. AI 모델의 사전학습 과정에서도 마찬가지로 "배치"의 의미를 효율성을 위해 모아서 학습시킨다고 생각했는데, 그게 아니라 배치 사이즈에 따라 학습 결과가 달라지는 하이퍼 파라미터라는 사실을 알게 되었습니다. 어떤 이유로 배치 사이즈가 훈련 결과에 영향을 미치는지 Gemini에게 물어봤고, 비유를 통해 답변을 들었지만 구체적인 코드나 수식을 통해 이해하진 못했습니다. 그 부분은 책을 더 읽어보면서 이해해볼 예정입니다.
4. 랜덤한 점들이 의미를 찾아가는 과정: 사과와 바나나는 어떻게 가까워지는가
- 질문
- 임베딩 층의 가중치를 왜 0이나 1이 아닌 랜덤 값으로 초기화하는가?
- 임베딩 층의 "가중치"란 무엇이며(중요도인가?), 이것이 "훈련된다"는 것은 구체적으로 어떤 과정인가?
- 답변 요약
- 랜덤 초기화 (Symmetry Breaking): 모두 같은 값으로 시작하면 똑같이 업데이트되어 학습이 안 되므로, 출발선을 다르게 하여 각자 다른 특징을 배우게 함.
- 가중치의 정체 (Lookup Table): 중요도가 아니라 단어 고유의 좌표값(Vector)을 저장한 테이블임.
- 훈련의 본질 (좌표 재배치): 초기에는 랜덤하게 흩뿌려진 단어들을, 문맥(데이터)을 보고 비슷한 단어(사과, 바나나)끼리는 가깝게, 다른 단어(자동차)는 멀게 좌표를 이동시키는 과정.
토큰화를 거친 후 임베딩 벡터로 변환하는 과정에서 뜬금없이 임베딩 층(layer)라고 부르는 행렬이 등장합니다. 이 행렬은 일종의 Lookup Table로 토큰의 번호 행에 그 토큰에 대응하는 벡터가 저장되어있습니다.
일단 저는 왜 초기값이 0이나 1이 아닌지 궁금했습니다. 보통 개발할 때 초기값은 0이나 1 혹은 의미있는 숫자로 지정해서 시작하는데 왜 랜덤 값으로 시작하는지 궁금했습니다. Gemini 의 답변을 듣고나서 떠올린 이미지는 자석 위에 종이를 얹고 그 위에 철가루를 뿌리면 처음에는 랜덤하게 퍼지지만 살살 종이를 흔들면 자기장 방향에 따라 철가루가 재배치되는 모습입니다. 철가루를 한 점에 모아두면 모양을 잡는데 오래걸리지만 전체에 흩뿌려 놓으면 좀 더 빨리 흐름을 형성하듯 단어별 벡터도 탐색 공간 내에 흩뿌려서 다양한 탐색을 하도록 의도했다고 이해했습니다.
임베딩 층(가중치 행렬)이 탐색 공간 내에서 단어별 좌표라고 생각하니 훈련의 의미도 쉽게 이해가 되었습니다. 훈련을 거치면서 단어 좌표가 움직이면서 서로 간의 인력과 척력에 의해 모이고, 멀어지는 것을 반복하는 이미지를 떠올릴 수 있었습니다. 어떻게 가까워지고 멀어지는지는 책을 더 읽어보면서 구체적으로 알아보겠습니다.
5. 행렬 곱셈 대신 인덱스 룩업: 수학적 동일성과 성능 최적화
- 질문
- 임베딩 층이 "원-핫 인코딩과 완전 연결 층(fully connected layer)의 행렬 곱셈"을 효율적으로 구현한 것이라는데 무슨 뜻인지?
- 답변 요약
- 수학적 동일성: 원-핫(one-hot) 변환은 토큰 ID 묶음을 행렬로 변환하는데, 한 행의 토큰 ID번째 숫자만 1(hot)이고 나머지는 0인 행렬로 변환. 완전 연결 층은 토큰 ID별 벡터를 저장한 행렬. 둘을 곱하면 토큰 ID별 벡터를 행렬 곱셈으로 얻을 수 있음.
- 효율성: 임베딩 층을 사용하여 인덱스 룩업하는 연산이 행렬 곱셈보다 빠름.
- 학습 가능성: 임베딩 층이 곧 신경망의 가중치이므로 일반 선형 층처럼 역전파를 통해 값을 학습하고 업데이트 할 수 있음.
임베딩 층을 거쳐 토큰 ID를 벡터로 변환하는 과정을 설명하다가 갑자기 "원-핫 인코딩"이라는 단어가 튀어나왔습니다. Gemini의 설명을 찬찬히 읽어보니 아래 그림을 떠올리고 이해할 수 있었습니다.
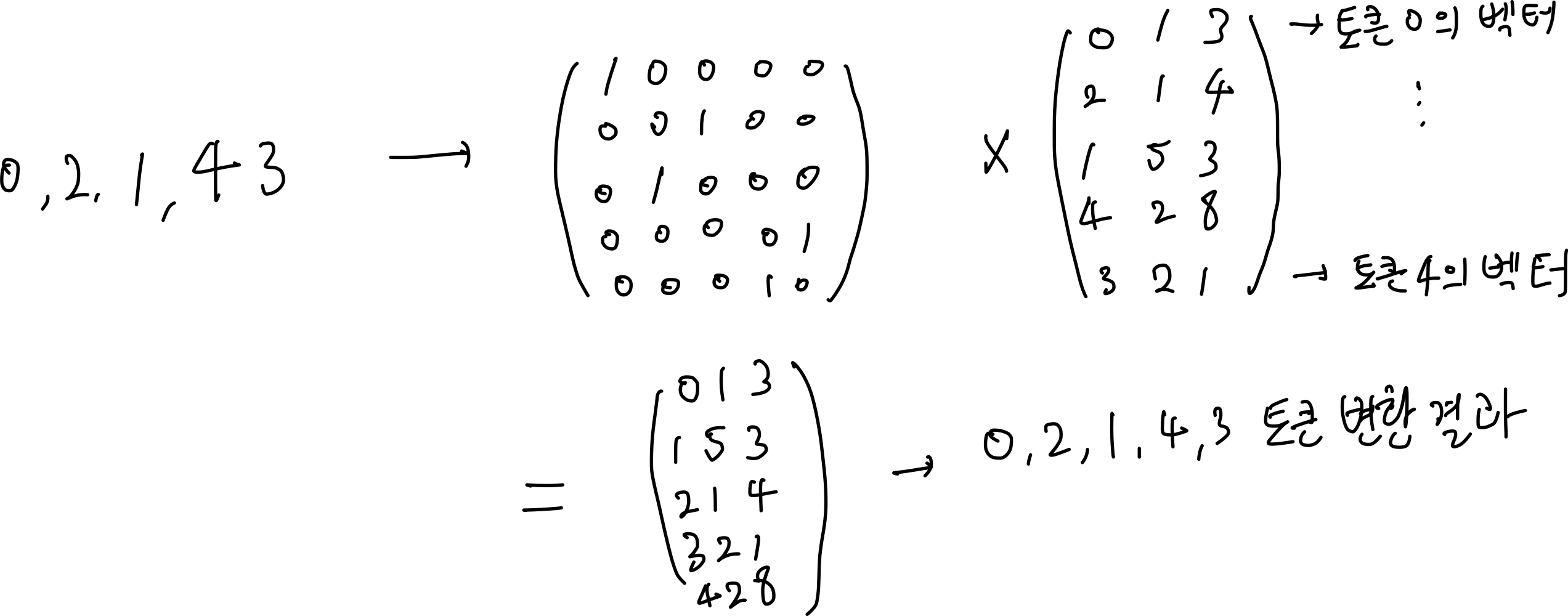
효율성 측면도 행렬 곱셈이 O(n^3)에 가까운 반면 인덱스 룩업은 O(1)으로 구현할 수 있으므로 이해가 되었습니다. 학습 가능성 측면은 아직 역전파 개념에 대해 잘 이해하고 있지 못해서 책을 좀 더 읽어보고 다시 알아보겠습니다.
마치며
서버 개발자로서 AI에 대한 지식 없이 책을 읽으면서 떠오르는 질문들을 하나씩 해결하고 있습니다. 왜 배치 크기가 결과에 영향을 미치는지, 임베딩 층의 가중치 행렬의 의미가 무엇인지 새롭게 알아가는 과정이 즐겁습니다.
결국 LLM이 문장을 이해한다는 것은, 수만 개의 단어가 저마다의 위치를 찾아가며 서로 밀고 당기는 거대한 균형의 지도를 그리는 일이라는 생각이 듭니다. 책을 더 읽어가면서 흩뿌려진 단어들이 서로를 어떻게 "주목(Attention)"하고 연결하는지 알아보겠습니다.
'기술' 카테고리의 다른 글
| 왜 더하고, 왜 자를까? 초고차원 공간에서 단어들이 자리를 잡는 법 (0) | 2026.01.09 |
|---|---|
| LLM 기초 해부: 토크나이저부터 단어 임베딩의 동적 분화까지 (0) | 2025.12.24 |
| 그래서 모나드가 뭔데? 타입 확장과 함수 합성의 관점에서 바라보기 (0) | 2025.12.18 |
| Kotlin JPA의 Entity에 val 필드를 사용해도 될까? (0) | 2025.12.18 |
| Kotlin에서 JPA 설정하기 총정리 (0) | 2025.12.18 |

